小学三年级下册数学奥数知识点讲解第2课《从哥尼斯堡七桥问题谈起》试题附答案

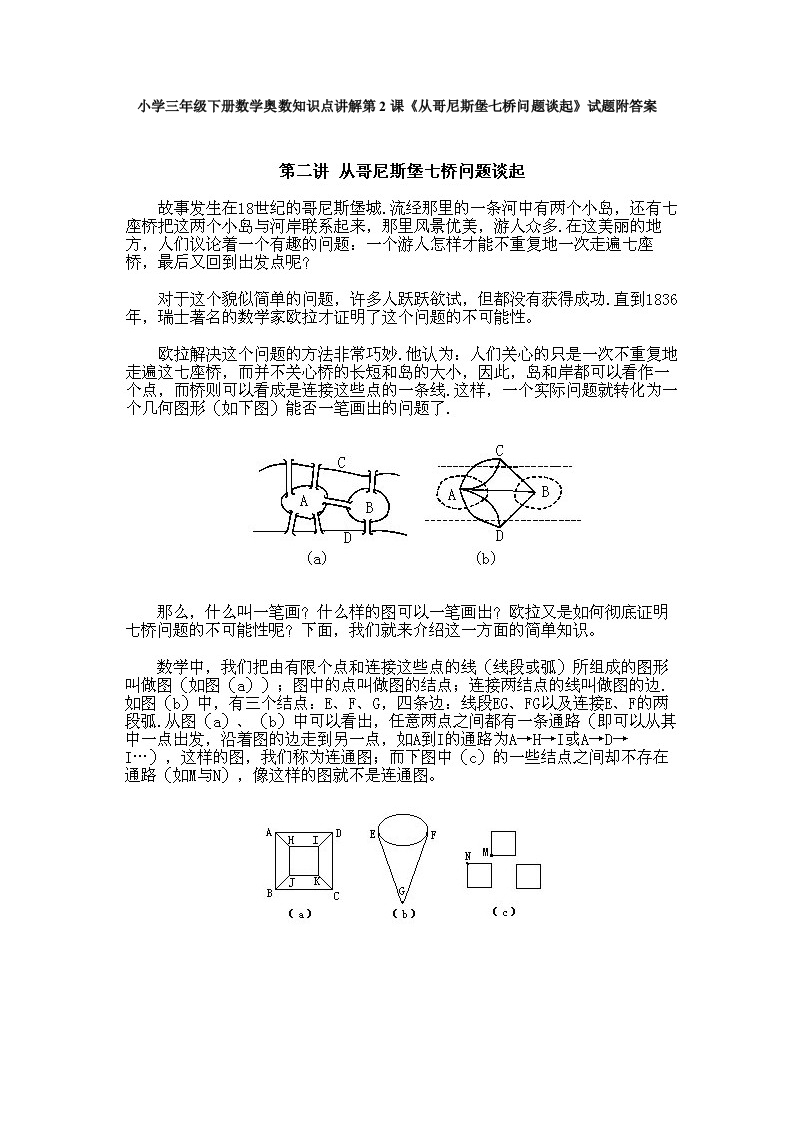
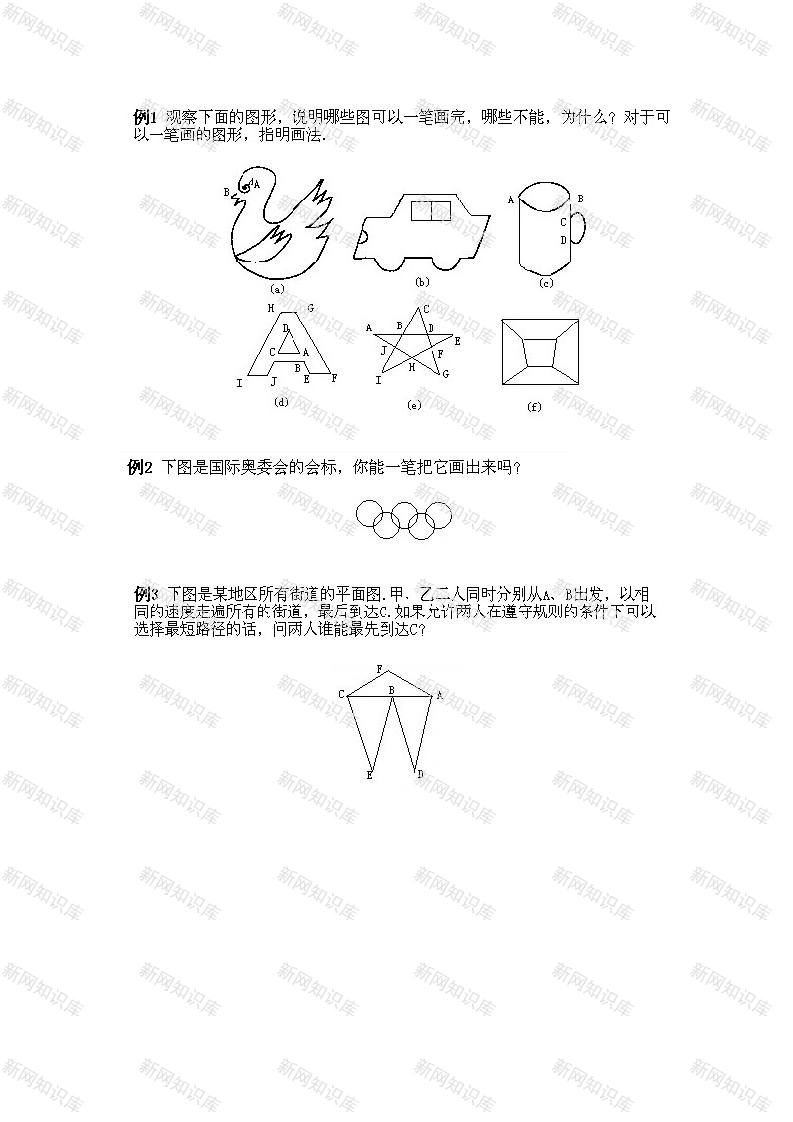
小学三年级下册数学奥数知识点讲解第2课《从哥尼斯堡七桥问题谈起》试题附答案第二讲从哥尼斯堡七桥问题谈起故事发生在18世纪的哥尼斯堡城.流经那里的一条河中有两个小岛，还有七座桥把这两个小岛与河岸联系起来，那里风景优美，游人众多.在这美丽的地方，人们议论着一个有趣的问题：一个游人怎样才能不重复地一次走遍七座桥，最后又回到出发点呢？对于这个貌似简单的问题，许多人跃跃欲试，但都没有获得成功.直到1836年，瑞士著名的数学家欧拉才证明了这个问题的不可能性。欧拉解决这个问题的方法非常巧炒.他认为：人们关心的只是一次不重复地走遍这七座桥，而并不关心桥的长短和岛的大小，因此，岛和岸都可以看作一个点，而桥则可以看成是连接这些点的一条线.这样，一个实际问题就转化为一个几何图形（如下图）能否一笔画出的问题了.(b)那么，什么叫一笔画？什么样的图可以一笔画出？欧拉又是如向彻底证明七桥问题的不可能性呢？下面，我们就来介绍这一方面的简单知识。数学中，我们把由有限个点和连接这些点的线（线段或弧）所组成的图形叫做图（如图（ā）)；图中的点叫做图的结点；连接两结点的线叫做图的边，如图(b)中，有三个结点：E、F、G,四条边：线段G、FG以及连接E、F的两段弧.从图（ā）、(b)中可以看出，任意两点之间都有一条通路（即可以从其中一点出发，沿着图的边走到另一点，如A到1的通路为A→H→I或A一→D一I…)，这样的图，我们称为连通图；而下图中(c)的一些结点之间却不存在通路（如与N),像这样的图就不是连通图。e)